16. Quiz: Landmarks
Map with Car Observations and Particle
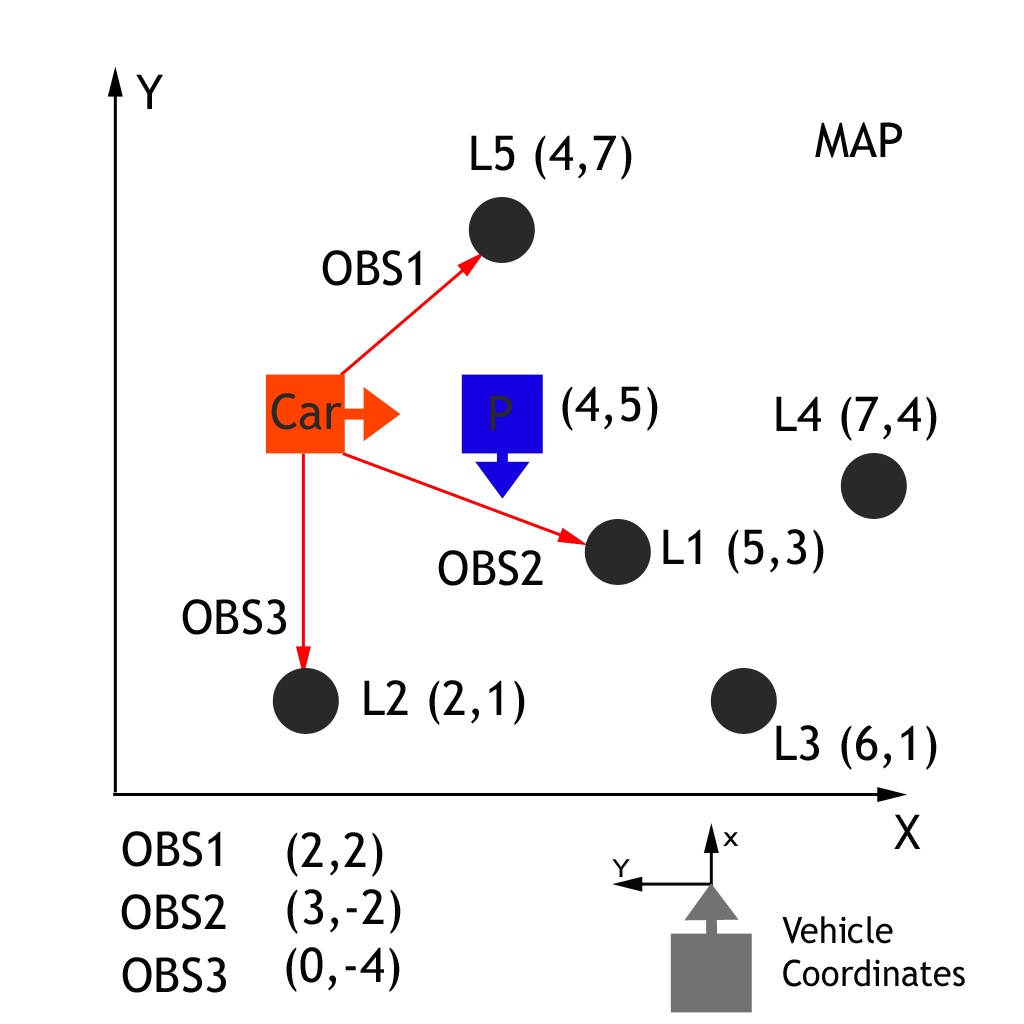
In the graph above we have a car ( ground truth position ) that observes three nearby landmarks, each one labeled OBS1, OBS2, OBS3. Each observation measurement has x, and y values in the car's coordinate system. We have a particle "P" ( estimated position of the car ) above with position (4,5) on the map with heading -90 degrees. The first task is to transform each observation marker from the vehicle's coordinates to the map's coordinates, with respect to our particle.
Transformations
There is a generalized trigonometric function that given any particle position and heading along with any observation measurement (x_obs,y_obs) will output the transformed observation (x_map,y_map) for that particle. In other words, we need to map particle coordinates to map coordinates, by passing particle and observation coordinates through a function.
Transformed Observation (x_map,y_map) = func(x_particle, y_particle, heading_particle, x_obs, y_obs)
You will need to derive and use this function to efficiently calculate particle observation transformations in the project.
- Some excellent resources discussing coordinate transformation and rotation matrices:
Transformation for OBS1
QUESTION:
OBS1 is the sensor observation reported from the sensor. As noted in the figure, OBS1 is (2,2). What is the position of OBS1 in map coordinates (x_map,y_map)? Enter your answer in parenthesis with the x value separated from the y value with a comma and no spaces.
SOLUTION:
NOTE: The solutions are expressed in RegEx pattern. Udacity uses these patterns to check the given answer
Transformation for OBS2
QUESTION:
OBS2 is the sensor observation reported from the sensor. As noted in the figure, OBS2 is (3,-2). What is the position of OBS2 in map coordinates (x_map,y_map)? Enter your answer in parenthesis with the x value separated from the y value with a comma and no spaces.
The answer does not match L2 - if you think it does, you need to check your work!
SOLUTION:
NOTE: The solutions are expressed in RegEx pattern. Udacity uses these patterns to check the given answer
Transformation for OBS3
QUESTION:
OBS3 is the sensor observation reported from the sensor. As noted in the figure, OBS3 is (0,-4). What is the position of OBS3 in map coordinates (x_map,y_map)? Enter your answer in parenthesis with the x value separated from the y value with a comma and no spaces.
SOLUTION:
NOTE: The solutions are expressed in RegEx pattern. Udacity uses these patterns to check the given answer
Resources, Hints, and Tips
- Without implementation of localization methods the car does not know where it is within an acceptable level of precision. The car knows particle coordinates and observation coordinates. The objective is to use the particle coordinates and heading to transform the car's frame of reference to the map's frame of reference, associate the observations, then use the associated observations in the map domain to update the particle weight.
- Since we know the coordinates of the particle from the car's frame of reference we can use this information and a matrix rotation/translation to transform each observation from the car frame of reference to the map frame of reference. The particle is at (4,5) in the map coordinate system with a heading of -90 degrees. The figure indicates the heading by depicting the particle x-axis as pointing down (blue arrow). This is critical to understanding the matrix transformation we are about to perform.
- By convention we define the car coordinate system with x pointing up and y rotated from x by pi/2 (+90 degrees). This is another way of saying that y is perpendicular and to the left of x. When x is pointing down, we have the mirror of this, with y perpendicular to the right. To visualize this make an L with your left index finger and thumb with palm facing away from you, this is our map frame of reference. Point the thumb towards the ceiling, this is the car coordinate convention, now point your thumb down, this is the orientation of the particle at (4,5).
- Now consider the map frame of reference (make an L with your left index finger and thumb as above), this is a typical presentation of Cartesian coordinates, with x pointing right and y perpendicular to the left, pointing up. If we rotate our thumb down we have the particle orientation. To get back to the map orientation we must rotate counterclockwise by 90 degrees (thumb from pointing down back to pointing right). Try this a few times with your left hand. Notice that particle to map is a counterclockwise rotation (+90 degrees) nd map to particle is a clockwise rotation (-90 degrees).
- The most straight forward way of rotating and translating coordinates is through homogenous transformation matrix (see below) using the angle of rotation required to get to the particle’s frame from the map’s point of view, -90 degrees. This way we can use theta directly. The alternative, which we will not cover here is to is to use -theta and a transformation matrix from the particle frame to the map frame.
- This video is a great resource for developing a deeper understanding of how to solve this transformation problem - it covers the rotation transformation, and from there you just need to perform a translation.
Observations in the car coordinate system can be transformed into map coordinates ( \text{x}_m and \text{y}_m ) by passing car observation coordinates ( \text{x}_c and \text{y}_c ), map particle coordinates ( \text{x}_p and \text{y}_p ), and our rotation angle (-90 degrees) through a homogenous transformation matrix. This homogenous transformation matrix, shown below, performs rotation and translation.
Homogenous Transformation
Matrix multiplication results in:
\text{x}_m= \text{x}_p + (\cos\theta \times \text{x}_c) - (\sin\theta \times \text{y}_c)
\text{y}_m= \text{y}_p + (\sin\theta \times \text{x}_c) + (\cos\theta \times \text{y}_c)